Cours de maths 3eme
Des cours gratuits de mathématiques de niveau collège pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Cours de maths 3eme
Cours sur les racines carrées
Définition et propriétés des racines carré
Définition et propriétés des racines carré
Définition
La racine carré d'un nombre a se note 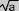 et correspond au nombre dont le carré vaut a
et correspond au nombre dont le carré vaut a
Une racine carrée ne peut être exister que pour un nombre a positif car il n'existe pas de nombre dont le carré à une valeur négative ( le produit de deux nombres de même signe est toujours positif )
Exemples:
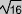 correspond au nombre dont le carré est 16 c'est à dire 4 ( puisque 4x4 = 16) donc
correspond au nombre dont le carré est 16 c'est à dire 4 ( puisque 4x4 = 16) donc 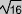 = 4
= 4
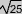 correspond au nombre dont le carré est 25 c'est à dire 5 ( puisque 5x5 = 25) donc
correspond au nombre dont le carré est 25 c'est à dire 5 ( puisque 5x5 = 25) donc 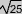 = 5
= 5
Racine carré d'un nombre élevé au carré et carré d'une racine carrée
Par définition le nombre dont le carré est a2 correspond à a donc 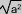 = a
= a
De même (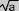 )2 = a
)2 = a
Exemples:
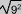 = 9
= 9
(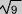 )2 = 9
)2 = 9
Nature d'une racine carrée
La racine carée d'un nombre peut être un nombre entier, un nombre décimale mais s'il elle n'appartient à aucune des deux catégories précédentes on dit qu'il s' agit d'un nombre irrationnel.
Exemples:
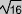 = 4 dont
= 4 dont 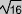 correspond à un entier
correspond à un entier
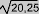 = 4,5 donc
= 4,5 donc 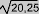 correspond à un nombre décimal
correspond à un nombre décimal
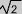 = 1,414213... donc
= 1,414213... donc 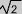 correspond à un nombre irrationnel
correspond à un nombre irrationnel
Vous souhaitez plus de cours sur ce sujet ? Faites-le nous savoir :

