Cours de maths 3eme

Des cours gratuits de mathématiques de niveau collège pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Cours de maths 3eme

Cours sur les inégalités et les inéquations

Résoudre une inéquation

Résoudre une inéquation

Méthode pour résoudre une inéquation
Pour résoudre une inéquation il faut suivre une méthode proche de celle de la résolution des équations.
Première étape: il faut simplifier au maximum les deux membres de l'inéquation en enlevant les parenthèses, en développant et en regroupant les termes de même nature.
Deuxième étape: Il faut éliminer l'inconnue (x) d'un des membres en ajoutant l'opposé du terme où elle intervient. Si ce terme est de forme ax alors on ajoute -ax au deux membres.
Troisiéme étape on élimine du membre où se trouve l'inconnu tous les autres termes. si on a un terme b alors on ajoute -b aux deux membres de l'inéquation.
Quatrième étape: on divise les deux membre par le coefficient de l'inconnu x. Attention: si ce coefficient est positif alors l'inéquation garde le même signe mais s'il est négatif alors le signe doit être inversé. Si on a un terme de type cx alors on divise les deux membres par c.
Dernière étape: il reste à traduire le résultats obtenus pour indiquer les solutions de l'inéquation.

Représentation des solutions d'une équation
On peut traduire les solutions d"une équation par une phrase mais il est plus fréquents de les représenter par un intervalle.
Si l'on obtient Une inéquation du type x < a alors la solution est l'intervalle situé avant x (à gauche) avec un crochet orienté vers l'extérieur de l'intervalle.

Si l'on obtient Une inéquation du type x > a alors la solution est l'intervalle situé après x (à droite) avec un crochet orienté vers l'extérieur de l'intervalle.

Si l'on obtient Une inéquation du type x 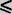  a alors la solution est l'intervalle situé avant x (à gauche) avec un crochet orienté vers l'intérieur de l'intervalle.

Si l'on obtient Une inéquation du type x 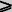a alors la solution est l'intervalle situé après x (à droite) avec un crochet orienté vers l'intérieur de l'intervalle.

Exemple de résolution d'inéquation
On souhaite résoudre l'inéquation 2x + 3(x +1) < 2-(x - 3)
On commence par simplifier les deux membres:
2x + 4(x +1) < 2-(2x - 8)
2x + 4x +4 < 2 - 2x + 8
6x +4 < 10 - 2x
Pour éliminer le terme -2x du membre de droite on ajoute 2x aux deux membres:
6x + 4 + 2x < 10 -2x +2x
8x + 4 < 10
Pour éliminer terme +4 du membre de gauche on ajoute -4 au deux membres:
6x + 4 +(-4) < 10 + (-4)
6x < 6
On divise les deux membres par 6 pour éliminer le facteur 6 de x
6x : 6 < 6 : 6
x < 1
On représente l'ensemble de solution par un intervalle: