Cours de maths 3eme

Des cours gratuits de mathématiques de niveau collège pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Cours de maths 3eme

Cours sur les fonctions linéaires et les fonctions affines

Les fonctions affines

Les fonctions affines

Qu'est-ce qu'une fonction affine ?
Une fonction affine est une fonction qui s'exprime sous la forme f(x)= ax +b où a et b peuvent être des nombres entiers, relatifs, décimaux ou fractionnaires.
Exemples
f(x) = 3x +1, f(x) = -9x + 12, f(x) = 10,5x - 5 ou f(x) = (2/3)x + 5,6 sont des fonctions affines.
Remarque: le terme a est aussi appelé coefficient directeur de la fonction affine et le terme b est souvent appelé ordonnée à l'origine.

Reconnaitre une fonction affine sur un graphique
Une fonction affine se représente toujours par une droite mais contrairement aux fonctions linéaires elle ne passe pas par l'origine.
Reciproquement si une fonction est représentée par une droite qui ne passe pas par l'origine alors on peut en conclure qu'il s'agit d'une fonction afine.


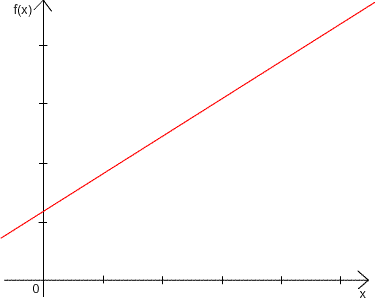
Déterminer l'expression d'une fonction afine
Pour connaître l'expression d'une fonction linéaire il faut déterminer son coefficient directeur a et son ordonnée à l'origine b.
Il faut connaître deux points pour pouvoir déterminer ces grandeurs.
Si A (x1; y1 ) et B ( x2 ; y2 ) sont solutions de l'équation d'une fonction linéaire alors:
- Il est possible de de trouver a et b grâce à un système de deux équations à deux inconnues:
y1 = ax1 + b
y2 = ax2 + b
Il suffit de résoudre les équations pour trouver a et b.
- Il est possible de déterminer la valeur de a en utilisant la relation
a = f(x2) - f(x1)      
         x2 - x1
b peut ensuite être trouvé en remplaçant a par sa valeur dans l'une des équations y1 = ax1 + b ou y2 = ax2 + b
- b peut être déterminer directement sur le graphique: b correspond à l'ordonée du point d'intersection de la droite avec l'axe des ordonnées.

Représenter une fonction afine
Puisque qu'une fonction afine est représentée par une droite il faut connaître deux de ses points pour pouvoir la tracer.
Le plus simple est de choisir dans un premier temps le point de coordonnées ( 0 ; b ) puis de déterminer un deuxième en utilisant son équation.