Cours de maths 3eme

Des cours gratuits de mathématiques de niveau collège pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Cours de maths 3eme

Cours sur le théorème de Thales

Le théorème de Thales

Le théorème de Thales

Enoncé du théorème de Thales
Si les points O, A, et B sont alignés d'une part, que les points O, C et D sont également alignés et que les droites AC et BD sont parallèles alors les égalités suivantes sont respectées:

Les deux cas d'application du théorème de Thales
Le Théorème de Thales peut s'appliquer dans deux type d'alignement des points
Cas n°1 les points O, A, B, C, et D constituent deux trinagles dont les cotés sont confondus:

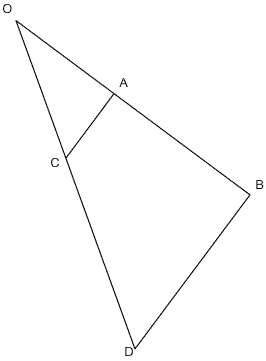
Cas n°2 Seul le sommet O est commun aux triangles OAC et OBD. Il s'agit de la configuration dite papillon

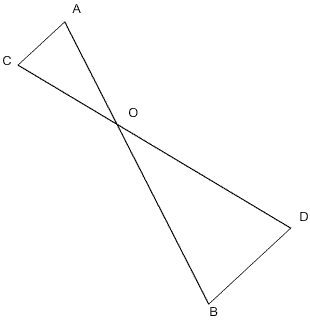
Utilisation du théorème de Thales
Le théorème de Thales peut être utilisé pour trouver une longueur inconnue.
Après avoir montré que les conditions d'utilisation du théorème sont réunies alors il faut choisir un rapport dont le numérateur et le dénominateur sont connus et un deuxième rapport faisant intervenir l'inconnue recherchée et une grandeur connue.
On obtient alors une équation avec une inconnue que l'on peut résoudre facilement.
Exemple:
On souhaite connaitre la valeur de AC sachant que AC est parallèle à BD.

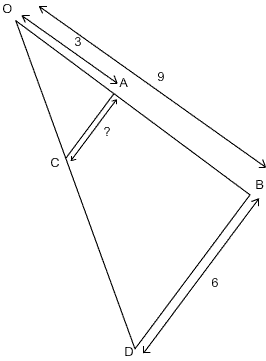
D'après le thèorème de Thales:
OA = OC = AC  
OB    OD    BD
On choisit un rapport connu :
OA = 3    
OB    9    

On choisit un rapport faisant intervenir l'inconnue ( AC ) et une grandeur connue:
AC = AC   
BD     6    
On écrit l'égalité:
AC = 3  
 6      9
On en tire AC = 3  x  6  
                        9
Donc AC = 2