Cours de maths 5eme
Des cours gratuits de mathématiques de niveau collège pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Cours de maths 5eme
Cours sur le prisme et le cylindre
Le prisme droit
Le prisme droit
Définition d'un prisme droit
Un prisme droit est solide constitué de deux faces identiques parallèles entre elles de forme polygonale ( rectangle, triangle, carré, pentagone etc ) qui constituent les bases du prisme. Il est également constitué de faces latérales rectangulaires toutes perpendiculaires aux bases.
Exemples de prisme droit
Exemple de prisme droit à base triangle:
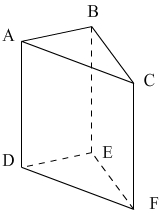
Dans cet exemple:
- ABC et DEF constituent les bases triangle du prisme
- ABED, BCFE et ACFD sont les faces latérales rectangulaires
- Les arêtes latérales DA, EB et FC correspondent à la hauteur du prisme.
- Les points A, B, C, D, E, F, sont les sommets du prisme.
Autres exemples:

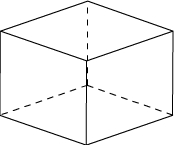
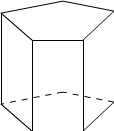
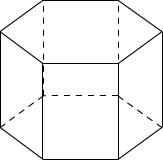
Remarque: un prisme droit dont la base est rectangulaire correspond à un pavé droit aussi appelé parallélépipède rectangle.
Aire latérale d'un prisme droit
L'aire latérale d'un prisme droit correspond à la somme des aire de toute les faces latérale.
Si l'on reprend l'exemle du prisme à base triangle alors son aire latérale correspond à la somme des aires des faces ABED, BCFE et ACFD.
L'aire latérale peut aussi se calculer en multipliant le périmètre d'une base par la auteur:
Dans l'exemple du prisme à base triangle l'aire latérale correspond au périmètre abc multiplié par le hauteur AD.
Volume d'un prisme droit
Le volume d'un prisme droit se calcule en multipliant l'aire d'une base par la hauteur:
Il faut faire attention aux unités utilisées. Si par exemple l'aire de la base est en cm2 alors la hauteur doit être exprimée en centimètre et le volume s'exprime en cm3. Si l'aire de la base est en mm2 alors la hauteur doit être exprimée en mm et le volume est alors en mm3 etc.
Vous souhaitez plus de cours sur ce sujet ? Faites-le nous savoir :

